JZX轻语:简
LeetCode 2718 - 查询后矩阵的和
发表于2024年09月10日
一开始的做法是先用哈希表记录每一行/每一列最后一次被修改的值以及修改”时间”(即操作的序号),然后遍历矩阵,对于每一个元素,判断它的最终值来源于最后一次的行修改还是列修改,然后累加即可。这个做法的时间复杂度是O(n^2),会超时。
但是,我们可以逆向思维,从最后一次操作开始,逐步向前。如果某一行/列在后面被修改了(可使用哈希表记录),就不再处理;否则,属于该行/列的最后一次修改,其影响的元素数目是n - 已经被修改的列/行数目。举个例子,如果当前处理某一行,此时已经有k列被修改了,那么这一行修改最终影响的元素数目就是n - k。这个做法的时间复杂度是O(n)。
以LeetCode官方示例n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]为例:
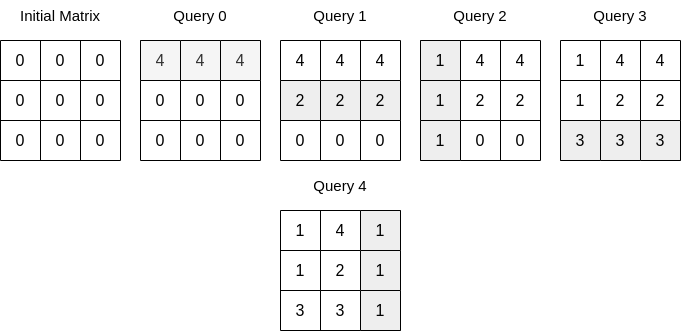
倒数第一次操作是
[1,2,1],即第2列被修改为1,那么第2列的最后一次修改最终影响的元素数目是3 - 0 = 3;此时,ans = ans + 1 * 3 = 3;倒数第二次操作是
[0,2,3],即第2行被修改为3,那么第2行的最后一次修改最终影响的元素数目是3 - 1 = 2;此时,ans = ans + 3 * 2 = 9;倒数第三次操作是
[1,0,1],即第0列被修改为1,那么第0列的最后一次修改最终影响的元素数目是3 - 1 = 2;此时,ans = ans + 1 * 2 = 11;倒数第四次操作是
[0,1,2],即第1行被修改为2,那么第1行的最后一次修改最终影响的元素数目是3 - 2 = 1;此时,ans = ans + 2 * 1 = 13;倒数第五次操作是
[0,0,4],即第0行被修改为4,那么第0行的最后一次修改最终影响的元素数目是3 - 2 = 1;此时,ans = ans + 4 * 1 = 17。
所以,最终的答案是17。
class Solution {
public:
using LL = long long;
LL matrixSumQueries(int n, vector<vector<int>>& queries) {
unordered_set<int> row_used, col_used;
LL ans = 0;
int type, index, val;
for (int i = queries.size() - 1; i >= 0; --i) {
const auto& query = queries[i];
type = query[0]; index = query[1]; val = query[2];
if (type == 0 && !row_used.count(index)) {
ans += val * (n - col_used.size());
row_used.insert(index);
} else if (type == 1 && !col_used.count(index)) {
ans += val * (n - row_used.size());
col_used.insert(index);
}
if (row_used.size() == n && col_used.size() == n) break;
}
return ans;
}
};Python的做法
class Solution:
def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
ans = 0
row_used = set()
col_used = set()
for type_, index, val in reversed(queries):
if type_ == 0 and index not in row_used:
row_used.add(index)
ans += val * (n - len(col_used))
elif type_ == 1 and index not in col_used:
col_used.add(index)
ans += val * (n - len(row_used))
if len(row_used) == n and len(col_used) == n:
break
return ans超时的版本:
class Solution:
def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
row_info = {}
col_info = {}
for t, (type_, index, val) in enumerate(queries):
if type_ == 0:
row_info[index] = (t, val)
else:
col_info[index] = (t, val)
ans = 0
for i in range(n):
for j in range(n):
rt, rval = row_info.get(i, (-1, 0))
ct, cval = col_info.get(j, (-1, 0))
val = rval if rt > ct else cval
ans += val
return ans